Note
Click here to download the full example code
Time and Amplitude Scaling [ex603.0]#
This example is published in [Wildhaber2020] .
Out:
Badly Conditioned Steady State Matrix W: Use larger boundaries or lower g.
Badly Conditioned Steady State Matrix W: Use larger boundaries or lower g.
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
import numpy as np
import lmlib as lm
from lmlib.utils import load_lib_csv_mc
def time_amplitude_scaling(Q, a, b):
q = np.arange(Q)
Mq = lm.poly_square_expo(q)
Mqp1 = lm.poly_int_expo(Mq)
L_int = lm.poly_int_coef_L(Mq)
L_eta = lm.mpoly_dilate_ind_coef_L(q) # matrix operation of vdiag
R_QQ = lm.permutation_matrix_square(Q, Q)
I_Q = np.eye(Q)
I_QQ = np.eye(Q ** 2)
c1 = L_int
c2 = np.kron(I_Q, L_int).dot(np.kron(L_eta, I_Q))
c3 = np.kron(I_QQ, L_int).dot(R_QQ).dot(np.kron(L_eta, L_eta))
bmaT = (np.power(b, Mqp1) - np.power(a, Mqp1)).T
A = bmaT @ c1
B = np.kron(I_Q, bmaT) @ c2
C = np.kron(I_QQ, bmaT) @ c3
return A, B, C, q, Mq
y = load_lib_csv_mc('SECG3_FILT_HP51_3CH_20S_FS2400HZ.csv', k_start=5500, K=750)
y = np.column_stack([np.convolve(y0, 1 / 50 * np.ones(50), 'same') for y0 in y.T])
fs = 2000
K = len(y)
t = np.arange(K)/fs
M = 3
Q = 5
ENERGY_THD = 60
ab_half = int((80e-3 * fs) / 2)
ks_alpha = np.array([370]) # fixing template
alssm = lm.AlssmPoly(poly_degree=Q - 1)
segment_right = lm.Segment(a=-ab_half, b=ab_half, direction=lm.BW, g=50, delta=ab_half)
cost = lm.CostSegment(alssm, segment_right)
rls = lm.RLSAlssmSetSteadyState(cost)
xs = rls.filter_minimize_x(y)
# generate template
dilate_factor = 1.456
amplitude_factor = 0.945
y_template = amplitude_factor * np.column_stack(
[np.interp(np.linspace(0, K, int(K * dilate_factor)), np.arange(K), y0) for y0 in y.T])
rls_tmpl = lm.RLSAlssmSetSteadyState(cost)
xs_tmpl = rls_tmpl.filter_minimize_x(y_template)
alphas = xs_tmpl[(ks_alpha * dilate_factor).astype(int)]
A, B, C, q, Mq = time_amplitude_scaling(Q, a=-ab_half, b=ab_half)
etas = np.linspace(0.5, 2, 1000)
J = np.full(K, np.inf)
cost_ratio = np.full(K, np.inf)
model_energy_obs = np.full(K, np.inf)
time_scaling_hat = np.full(K, np.nan)
amplitude_hat = np.full(K, np.nan)
for k in range(K):
beta_beta = np.zeros(Q ** 2)
alpha_beta = np.zeros(Q ** 2)
alpha_alpha = np.zeros(Q ** 2)
for m in range(M):
beta_beta += np.kron(xs[k, :, m], xs[k, :, m])
alpha_beta += np.kron(alphas[0, ..., m], xs[k, :, m])
alpha_alpha += np.kron(alphas[0, ..., m], alphas[0, ..., m])
a1 = A @ beta_beta
for eta in etas:
J_ = a1 - (((B @ alpha_beta).T @ np.power(eta, q)) ** 2) / ((C @ alpha_alpha).T @ np.power(eta, Mq))
if J_ < J[k]:
J[k] = J_
time_scaling_hat[k] = eta
amplitude_hat[k] = ((B @ alpha_beta).T @ np.power(eta, q)) / ((C @ alpha_alpha).T @ np.power(eta, Mq))
cost_ratio[k] = J_/a1
model_energy_obs[k] = a1
mask = ENERGY_THD < model_energy_obs
k_range_mask = np.flatnonzero(mask)
k_min = k_range_mask[np.argmin(cost_ratio[mask])]
L_dilate = lm.poly_dilation_coef_L(np.arange(Q), time_scaling_hat[k_min])
alphas_hat = amplitude_hat[k_min]*np.einsum('jn, knm->kjm', L_dilate, alphas)
offset_channels = np.arange(M) + 1
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, gridspec_kw={'width_ratios': [1, 2, 2]})
ab_half_ext = int(ab_half * 1.15)
segment_right = lm.Segment(a=-ab_half_ext, b=ab_half_ext, direction=lm.BW, g=50, delta=ab_half_ext)
cost_ext = lm.CostSegment(alssm, segment_right)
segment_k, trajs_tmpl = cost.trajectories(alphas)[0][0]
trajs_obs = lm.map_trajectories(cost.trajectories(xs[ks_alpha]), ks_alpha, K, True, True)
trajs_tmpl_hat = lm.map_trajectories(cost.trajectories(alphas_hat), [k_min], K, True, True)
trajs_obs_ext = lm.map_trajectories(cost_ext.trajectories(xs[ks_alpha]), ks_alpha, K, True, True)
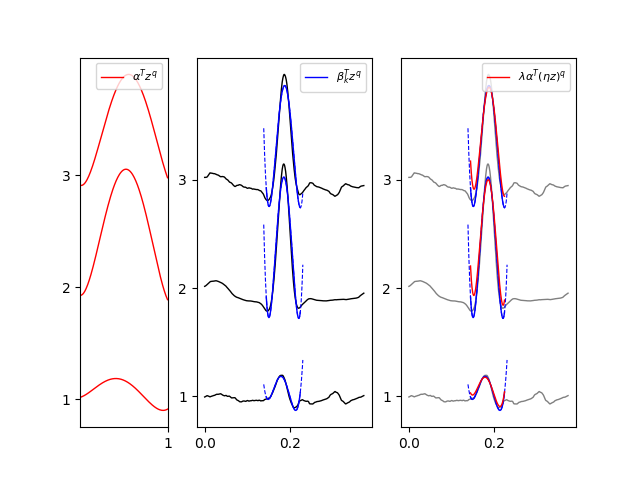
ax1.plot(segment_k, trajs_tmpl + offset_channels, lw=1, c='r', label=r'$\alpha^T z^q$')
ax1.set_xlim([min(segment_k), max(segment_k)])
ax1.set_xticks([max(segment_k)])
ax1.set_xticklabels(['1'])
ax1.legend([Line2D([0], [0], color='r', lw=1)], [r'$\alpha^T z^q$'], loc=1, fontsize=8)
ax2.plot(t, y + offset_channels, lw=1, c='k')
ax2.plot(t, trajs_obs_ext + offset_channels, lw=0.8, ls='--', c='b')
ax2.plot(t, trajs_obs + offset_channels, lw=1, c='b')
ax2.legend([Line2D([0], [0], color='b', lw=1)], [r'$\beta_k^T z^q$'], loc=1, fontsize=8)
ax3.plot(t, y + offset_channels, lw=1, c='grey')
ax3.plot(t, trajs_obs_ext + offset_channels, lw=0.8, ls='--', c='b')
ax3.plot(t, trajs_obs + offset_channels, lw=1, c='b')
ax3.plot(t, trajs_tmpl_hat + offset_channels, lw=1, c='r', label=r'$\alpha^T z^q$')
ax3.legend([Line2D([0], [0], color='r', lw=1)], [r'$\lambda \alpha^T (\eta z)^q$'], loc=1, fontsize=8)
for ax in fig.axes:
ax.set_yticks([1, 2, 3])
plt.show()
# show cost and estimate over time
if True:
fig, axs = plt.subplots(5, 1, sharex='all')
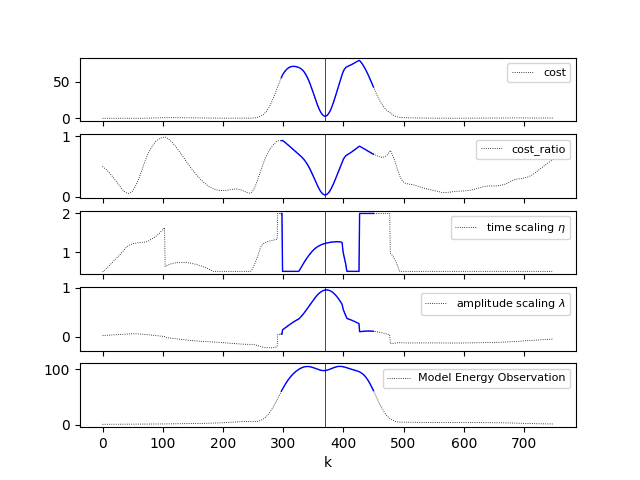
axs[0].plot(J, c='k', lw=0.6, ls=':', label='cost')
axs[0].plot(k_range_mask, J[mask], c='b', lw=1)
axs[1].plot(cost_ratio, c='k', lw=0.6, ls=':', label='cost_ratio')
axs[1].plot(k_range_mask, cost_ratio[mask], c='b', lw=1)
axs[2].plot(time_scaling_hat, c='k', lw=0.6, ls=':', label=r'time scaling $\eta$')
axs[2].plot(k_range_mask, time_scaling_hat[mask], c='b', lw=1)
axs[3].plot(amplitude_hat, c='k', lw=0.6, ls=':', label=r'amplitude scaling $\lambda$')
axs[3].plot(k_range_mask, amplitude_hat[mask], c='b', lw=1)
axs[4].plot(model_energy_obs, c='k', lw=0.6, ls=':', label=r'Model Energy Observation')
axs[4].plot(k_range_mask, model_energy_obs[mask], c='b', lw=1)
for ax in axs:
ax.axvline(k_min, c='k', lw=0.5)
ax.legend(loc=1, fontsize=8)
axs[-1].set_xlabel('k')
plt.show()
Total running time of the script: ( 0 minutes 4.803 seconds)